Short Answer Questions - II - 3 Marks
Q1. Give three examples when the object is not displaced in spite of a force acting on it.
Ans. Three examples when force being supplied and still there is no displacement are:
(i) A man pushing a stationary truck.
(ii) A man pushing a rigid wall.
(iii) A boy carrying a basket on his head and standing still. Here, force of gravity acts on the basket, but there is no displacement.
Q2. What types of energy transformation takes place in the following:
(i) Electric heater
(ii) Solar battery
(iii) Dynamo
(iv) Steam engine and
(v) Hydroelectric power station?
Ans.
(i) Electric heater: Electric energy into heat energy.
(ii) Solar battery: Solar energy into electric energy.
(iii) Dynamo: Mechanical energy into electric energy.
(iv) Steam engine: Heat energy to mechanical energy.
(v) Hydroelectric power station: Mechanical energy into electric energy.
Q. 3. (a) Derive an expression for kinetic energy of an object.
(b) If the velocity of an object is doubled. What will be change in its kinetic energy?
Ans. Suppose a body of mass m is moving with velocity v. It is brought to rest by applying a retarding force F. Suppose it traverses a distance s before coming to rest.
Kinetic energy of body, KE = Work done by retarding force to stop it.
i.e., Kinetic energy = F. s … (i)
But Retarding force, F = ma … (ii)
Initial velocity = v, final velocity = 0
From the equation, v2 = u2 + 2as, we have
0 = v2 – 2as (because here a is retardation)
⟹ Distance,s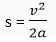 
… (iii)
Substituting values of F and s from (ii) and (iii) in (i), we get
Kinetic energy,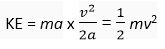 
Q. 4. A rocket is moving up with a velocity v. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies?
Ans. Initial velocity = v, then final velocity, v’ = 3v
Initial kinetic energy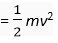 
Final kinetic energy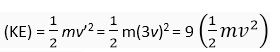 
(KE) initial: (KE) final = 1 : 9.
Q5. Avinash can run at a speed of 8 ms-1 against the frictional force of 10 N, and Kapil can move at a speed of 3 ms-1 against the frictional force of 25 N. Who is more powerful and why?
Ans. Power of Avinash PA = F A .v A = 10 x 8 = 80 W
Power of Kapil PK . FK . vK = 25 x 3 = 75 W
So, Avinash is more powerful than Kapil.
Q. 6. The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
Ans.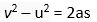 
This gives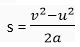 
F = ma
We can write work done (W) by this force F
W = Fs
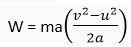
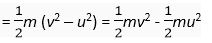
= Final KE - Initial KE.
Q7. (a) Give one example of each of the following:
(i) Small mass but high kinetic energy
(ii) Large mass but low kinetic energy
(b) Prove mathematically that the total mechanical energy of a freely falling body in air is conserved.
Ans.
(a) (i) A cricket/hockey ball which has been hit hard and is travelling fast.
(ii) A shot put thrown by an athlete
(b) Let the body of mass m at height h above the ground starting from rest, be falling freely.
Total energy of the body at height h
= mgh (PE) + 0 (KE) = mgh
After the body has fallen freely through a distance x (say),
KE = mgh, PE = mg (h – x)
Total energy = KE + PE
= mgh + mg (h – x) = mgh
When it reaches the ground 
PE = 0, Total Energy = KE + PE = mgh
Thus, the total mechanical energy, which is the sum of KE and PE is always equal to mgh.
Q8. Figure shows, in order, five stages of an athlete successfully performing a pole-vault.
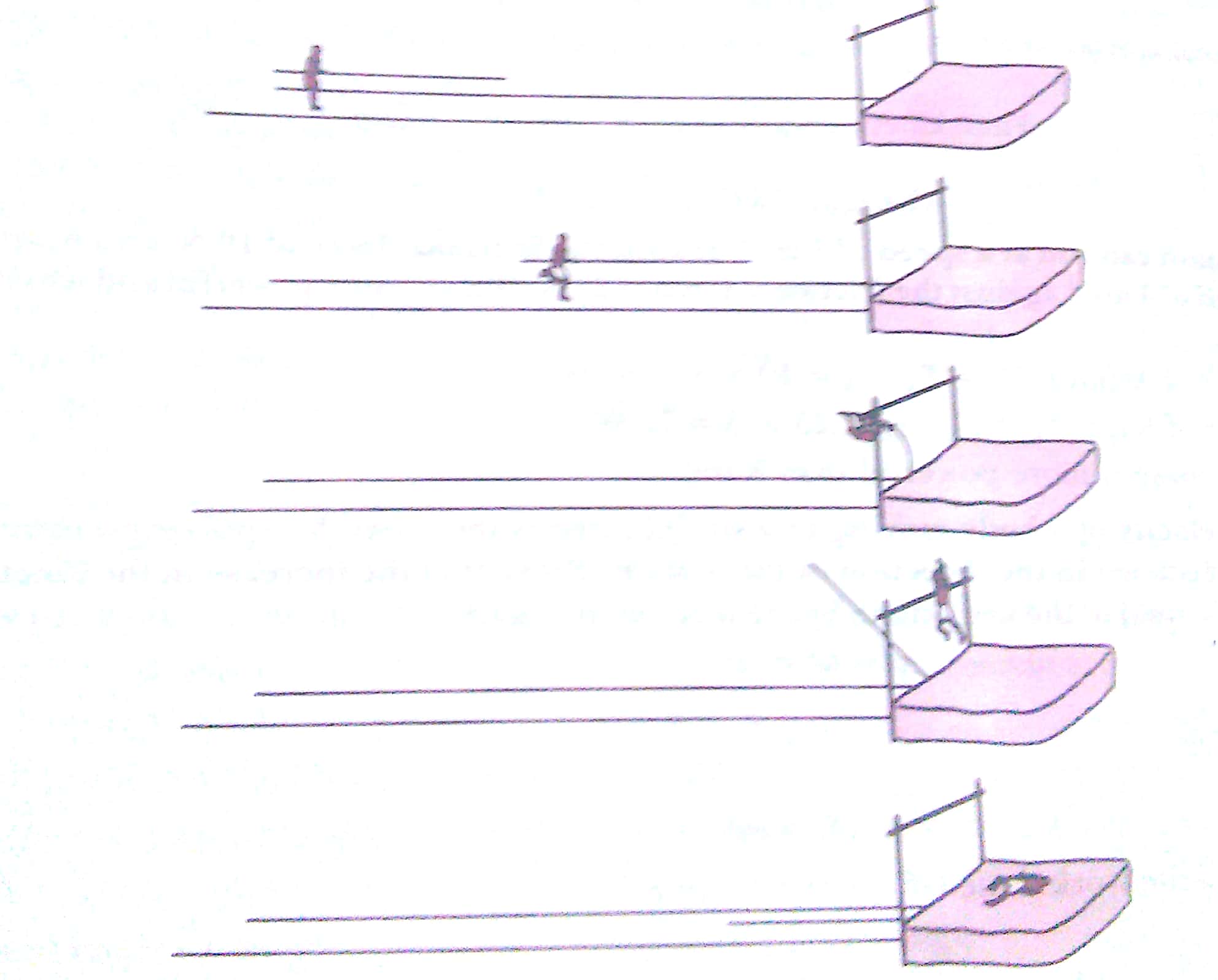
Describe the energy changes which take place during the performance of the pole-vault, from the original stationary position of the pole-vaulter before the run-up, to the final stationary position after the vault.
Ans.
Standing : Chemical energy
Run-up : Kinetic energy
Pole bent : Elastic energy
Rise : Potential energy gained
Fall : Kinetic energy gained
On mat : Heat or sound energy
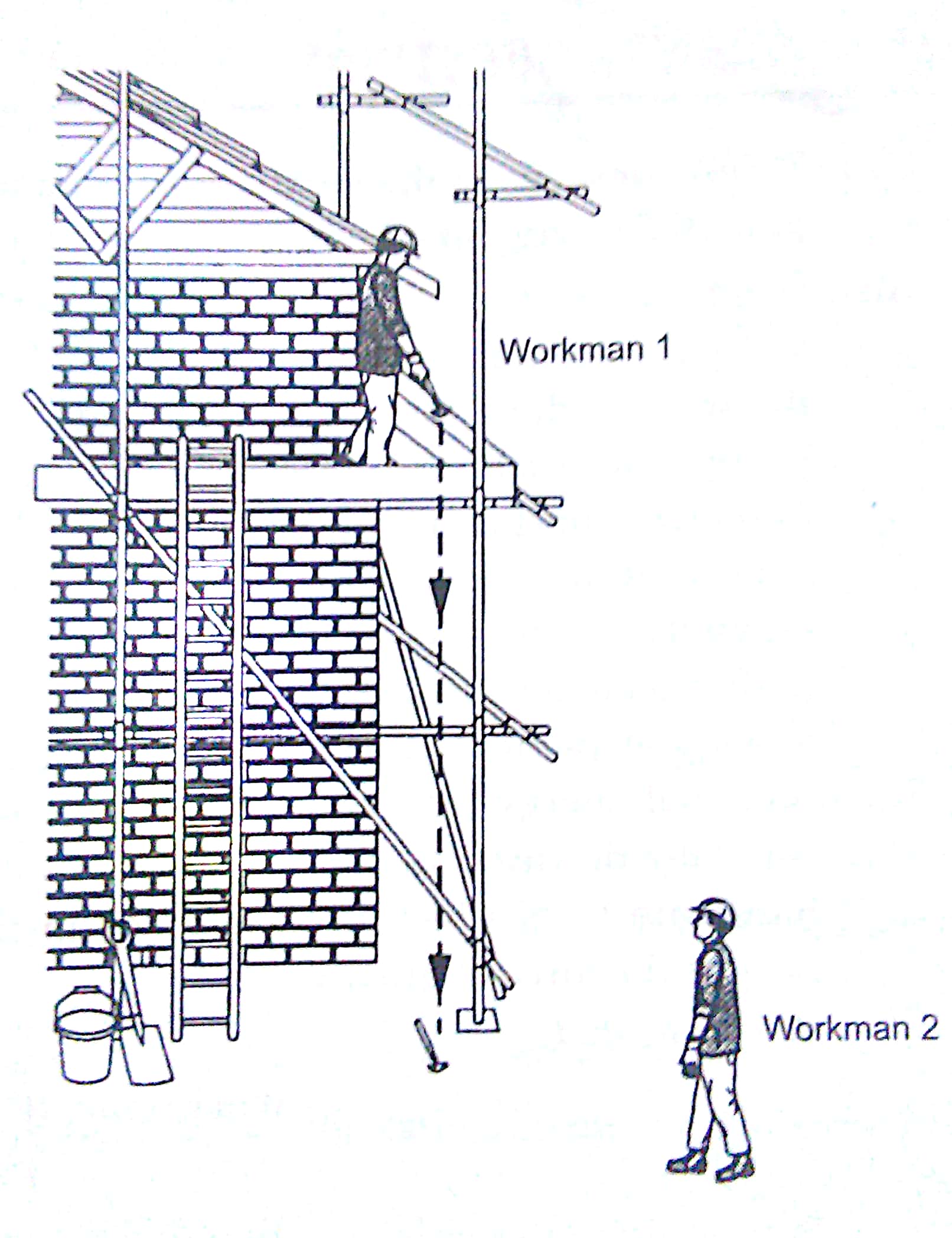
Q9. Two workmen are employed on a building project, as shown in figure.
(i) Workman 1 drops a hammer, which falls to the ground. The hammer has a mass of 2.0 kg, and is dropped from a height of 4.8 m above the ground.
(a) Calculate the change in gravitational potential energy of the hammer when it is dropped.
(b) Describe the energy changes from the time the hammer leaves the hand of workman 1 until it is at rest on the ground.
(ii) Workman 2 picks up the hammer and takes it back, up the ladder to workman 1. He climbs the first 3.0 m in 5.0 s. His total weight, including the hammer, is 520 N. Calculate the useful power which his legs are producing.
Ans.
(i) (a) Mass, m = 2.0 kg, height, h = 4.8 m
Change in gravitational potential energy
= mgh
=2 × 10 × 4.8 = 96 J
(b) Potential energy
(ii) Weight, mg = 520 N, height, h = 3.0 m, Time, t = 5.0 s
Useful power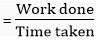 
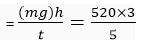
= 312 W
Q10.
(a) A body thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and final points of the path of the object lie on the same horizontal line. What is the work done by the force of gravity on the object?
(b) You lift a heavily packed carton of mass m in vertically upward direction through a height h. What is the work done (i) by you on the carton, (ii) by force of gravity on the carton?
(c) Anil is doing work at a rapid rate but works for only one hour. Ashok does work at a somewhat slower rate but continues to work for six hours. Who has greater power? Who has more energy?
Ans.
(a) Work done is zero. This is because equal and opposite work is done in the two paths.
(b) (i) Work done by me is positive and having a value = mgh. This is because I am applying force in vertically upward direction on the carton to hold it and displacement is also in the same direction.
(ii) Work done by the force of gravity on the carton = - mgh. This in because force is vertically downward but motion is vertically upward.
(b) Anil has greater power because his rate of doing work is more. Ashok has more energy as he worked for a longer time and the total work done by him in definitely more.