Short Answer Questions – I - 2 Marks
Q1. Give two examples from everyday life where work is done.
Ans.
(i) We apply a force to lift a book at a height and the book rises.
(ii) When a bullock pulls a cart, it moves as work is done by the bullock on the cart.
Q2. On what factors the work done on a body depends?
Ans. The work done on a body depends upon two factors:
(i) Magnitude of the force (F), and
(ii) The displacement through which the body moves (s).
Q3. What is energy? What is unit of energy?
Ans. The capacity of a body to do work is called energy possessed by the body. Itis a scalar quantity and is measured in joule (J).
Generally, for practical purposes, a bigger unit called kilojoule (kJ) is used (1 kJ = 1000 J).
Q4. Give any two uses of kinetic energy.
Ans. (i) The kinetic energy of air is used to run windmills.
(ii) The kinetic energy of the running water is used to generate electricity.
Q5. Give one example each of potential energy (i) due to position (ii) due to shape.
Ans. (i) Potential energy due to position: Water stored in dam has potential energy.
(ii) Potential energy due to shape: In a toy car, the wound spring possesses potential energy, and as the spring is released, its potential energy changes into kinetic energy due to which the car moves.
Q6. (a) What kind of energy transformation takes place when a body is dropped from a certain height?
Ans. When a body falls, its potential energy gradually gets converted into kinetic energy. On reaching the ground, the whole of the potential energy of the body gets converted into kinetic energy.
(b) What is the commercial unit of energy?
Ans. The commercial unit of energy is kilowatt hour [kWh].
1 kWh is the energy used in one hour at the rate of 1000 Js-1.
Q7. What is the relationship between the commercial unit and SI unit of energy?
Ans. We know that,
1kWh = 1kW x 1 h
= 1000 W x 3600 s
= 1000 Js-1 x 3600 s
= 3600000 J
∴ 1kWh = 3.6 x 106J
Q. 8. Calculate the work done against the gravity.
Ans. Suppose a body of mass m is lifted vertically upwards through a distance h. In this case, the force required to lift the body will be equal to weight of the body, mg (where m is mass and g is acceleration due to gravity), Now,
Work done in lifting a body = Weight of body x Vertical distance
W = mg × h
= mgh
Where W = Work done, and h = Height through which the body is lifted.
Q. 9. What is power? How do you differentiate kilowatt from kilowatt hour?
Ans. Power is the rate of doing work. Kilowatt is the unit of power and kilowatt hour is the unit of energy.
Q. 10. Observe the diagrams I and II carefully. An object of mass m is lifted from A to B to height h along path 1 and path 2. What would be the work done on the object in both the
cases? Give reasons for your answer.
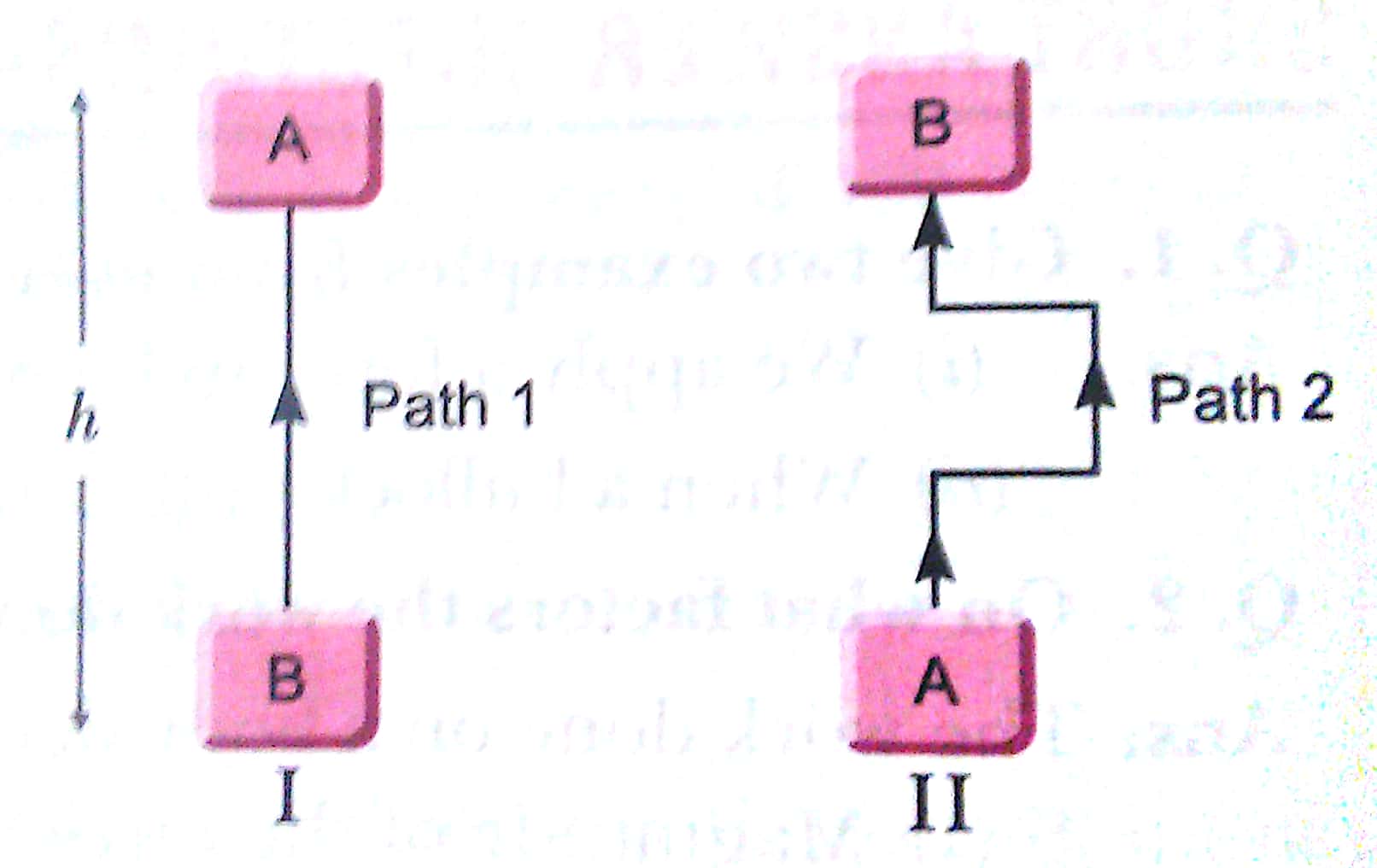
Ans. Work done in diagram I = mgh. Work done in diagram II = mgh. Work done by gravity depends on the differences in vertical heights of the initial and final positions of the object and not on the path along which the object is moved.

