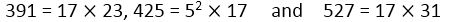Real Numbers
Que 1. Show that there is no positive integer n for which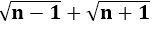 
is rational.
Ans. Let there be a positive integer n for which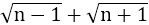 
be rational number.
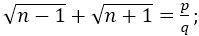where p, q are integer and q 
0 ……(i)
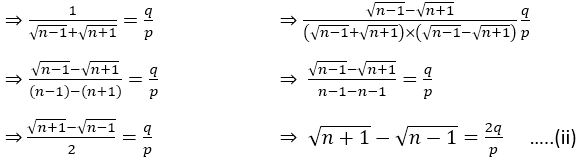
Adding (i) and (ii), we get
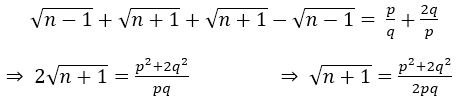
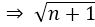is rational number as 
n + 1 is perfect square of positive integer …(A)
Again subtracting (ii) from (i), we get
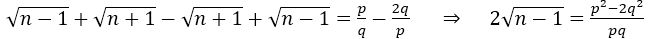
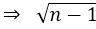is rational number as 
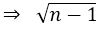is also perfect square of positive integer .....(B)
From (A) and (B)
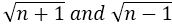are perfect squares of positive integer. It contradict the fact that two perfect differ at least by 3.
Hence, there is no positive integer n for which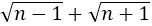 
is rational.
Que 2. Let a, b, c, k be rational numbers such that k is not a perfect cube.
If a + bk1/3 + ck2/3 = 0, then prove that a = b = c = 0.
Ans.
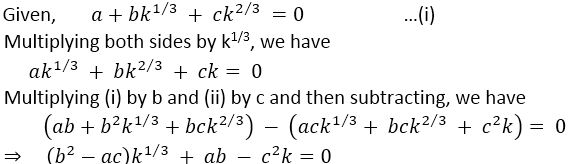
Que 3. Find the largest positive integer that will divide 398, 436 and 542 leaving remainders 7, 11 and 15 respectively.
Ans. It is given that on dividing 398 by the required number, there is a remainder of 7. This means that 398 – 7 = 391 is exactly divisible by the required number. In other words, required number is a factor of 391.
Similarly required positive integer is a factor of 436 – 11 = 425 and 542 – 15 = 527.
Clearly, required number is the HCF of 391, 425 and 527.
Using the factor tree we get the prime factorisations of 391, 425 and 425 and 527 as follows: 
