Long Answer Questions - 5 Marks

Q. 1. Derive expression for force of attraction between two bodies and then define gravitational constant.

Ans. "Everybody in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them." Let us consider two bodies A and B of masses m₁ and m₂ which are separated by a distance r. Then the force of gravitation (F) acting on the two bodies is given by
                                  F ∝ m₁× m₂                                                         … (1)

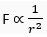
and                                                                           … (2)

Combining (1) and (2), we get

                                      

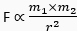
Or 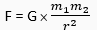                                                                   … (3)

where G is a constant known as universal gravitational constant.

Here, if the masses m₁ and m₂ of the two bodies are of 1 kg and the distance (r) between them is 1 m, then putting m₁ = 1 kg, m₂ = 1 kg and r = 1m in the above formula, we get

                                           G = F

Thus, the gravitational constant G is numerically equal to the force of gravitation which exists between two bodies of unit masses kept at a unit distance from each other.

 

Q. 2. Define acceleration due to gravity. Derive an expression for acceleration due to gravity in terms of mass of the earth (M) and universal gravitational constant (G).

Ans. The acceleration produced in the motion of a body falling under the force of gravity is called acceleration due to gravity. It is denoted by 'g'
The force (F) of gravitational attraction on a body of mass m due to earth of mass M and radius R is given by

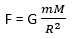                                                                                     … (1)                                      

We know from Newton's second law of motion that the force is the product of mass and acceleration.

  ∴                                                                       F = ma

But the acceleration due to gravity is represented by the symbol g. Therefore, we can write

                                                         F = mg                                  … (2)

From the equation (1) and (2), we get

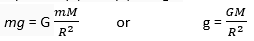                                                    … (3)

When body is at a distance 'r' from centre of the earth then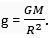 

Q. 3. Show that the weight of an object on the moon is th of its weight on the earth.

Ans. Suppose the mass of the moon is M_m and its radius is R_m. If a body of mass m is placed on the surface of moon, then weight of the body on the moon is

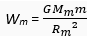                                                                                   … (1)

Weight of the same body on the earth's surface will be

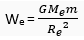                                                                                       … (2)

where M, = mass of earth and R_e radius of earth.

Dividing equation (1) by (2), we get

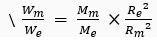                                                                          … (3)

Now, mass of the earth, M_e = 6 x 10²⁴ kg

mass of the moon, M_m = 7.4 x 10²² kg

radius of the earth, R _e = 6400 km

and radius of the moon, R_m = 1740 km

Thus, equation (3) becomes,

                               

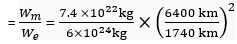
Or                            

The weight of the body on the moon is about one-sixth of its weight on the earth.

Q. 4. How does the weight of an object vary with respect to mass and radius of earth? In a hypothetical case, if the diameter of the earth becomes half of its present value and its mass becomes four times of its presents value, then how would the weight of any object on the surface of the earth be affected?  

Ans. Weight of an object is directly proportional to the mass of earth and inversely proportional to the square of the radius of the earth. i.e.,

                          Weight of a body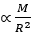 

                          Original weight,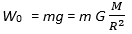 

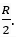
When hypothetically M becomes 4 M and R becomes 

Then weight becomes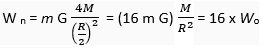 

The weight will become 16 times.