Long Answer Questions - 5 Marks

Q1. with the help of a graph, derive the relation v = u + at.

Ans. Consider the velocity-time graph of an object that moves under uniform acceleration as shown in the figure (u O).

From this graph, we can see that initial velocity of the object (at point A) is u and then it increases to v (at point B) in time t. The velocity changes at a uniform rate a. As shown in the figure, the lines BC and BE are drawn from point B on the time and the velocity axes respectively, so that the initial velocity is represented by OA, the final velocity is represented by BC and the time interval t is represented by OC. BD = BC - CD, represents the change in velocity in time interval t.

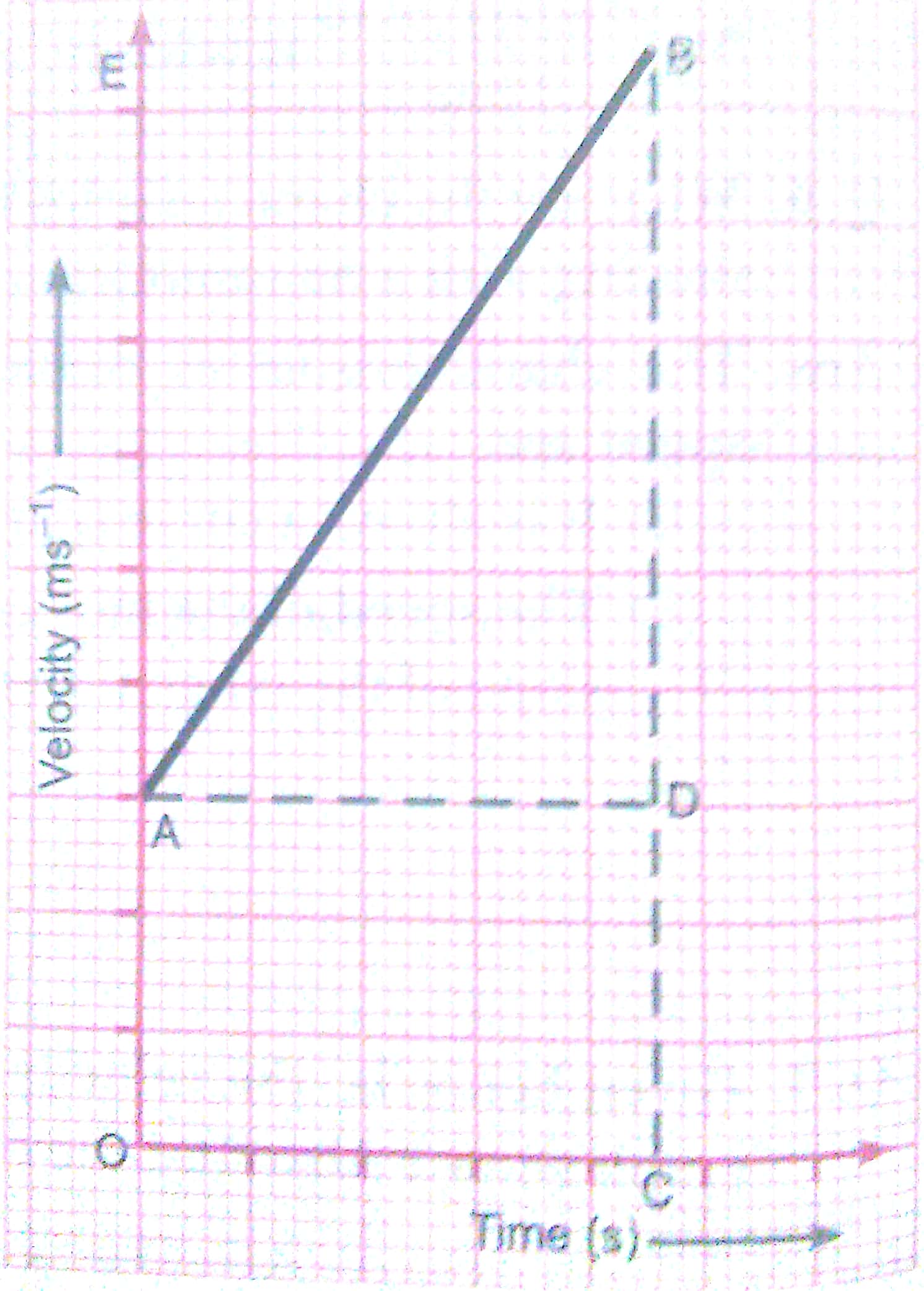
If we draw AD parallel to OC, we observe that
BC = BD + DC = BD + OA
Substituting, BC with v and OA with u,
we get
       v = BD + u
or   BD = v - u
Thus, from the given velocity-time graph, the acceleration of
the object is given by

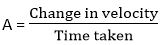
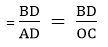
Substituting, OC with t, we get

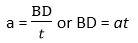
From equations (1) and (2), we have

v – u = at   or   v = u + at

Q. 2. Deduce the following equations of motion:

Ans. (i) Consider a body which starts with initial velocity u and due to uniform acceleration a, its     final velocity becomes v after time t. Then, its average velocity is given by

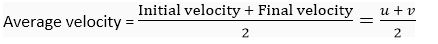
∴       The distance covered by the body in time t is given by
          Distance, s = Average velocity x Time

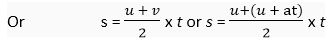
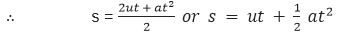
(ii) we know that

Putting the value of t in (1), we have

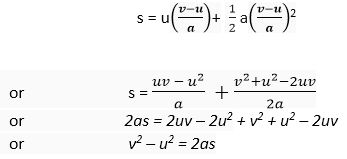
Q.3. Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4^th and 5^th seconds.

Ans. Using the equation of motion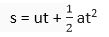 

Distance travelled in 5 seconds,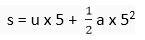  

Or                                                

similarly, distance travelled in 4 seconds'

Distance travelled in the interval between 4^th and 5^th seconds

                                              

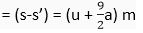
Q. 4. Two stones are thrown vertically upwards simultaneously with their initial velocities u₁ and u₂ respectively. Prove that the heights reached by them would be in the ratio of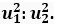

(Assume upward acceleration is -g and downward acceleration to be + g).

Ans. We know the upward motion,

But at highest point                           v = 0

Therefore,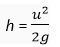                                          

For first ball,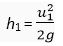                                   

And for second ball,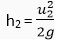                        

Thus,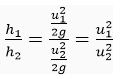                                              

Or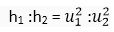                                                 

Q. 5. The driver of train A travelling at a speed of 54 kmh^-1 applies brakes and retards the train uniformly. The train stops in 5 seconds. Another train B is travelling on the parallel with a speed of 36 kmh^-1. Its driver applies the brakes and the train retards uniformly; train B stops in 10 seconds. Plot speed-time graphs for both the trains on the same axis. Which of the trains travelled farther after the brakes were applied?

Ans. For train A, the initial velocity,

                     

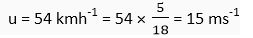
Final velocity, v = 0 and time, t = 5s

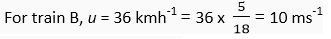
                   v = 0; t =10 s

Speed-time graph for train A and B are shown in the figure.

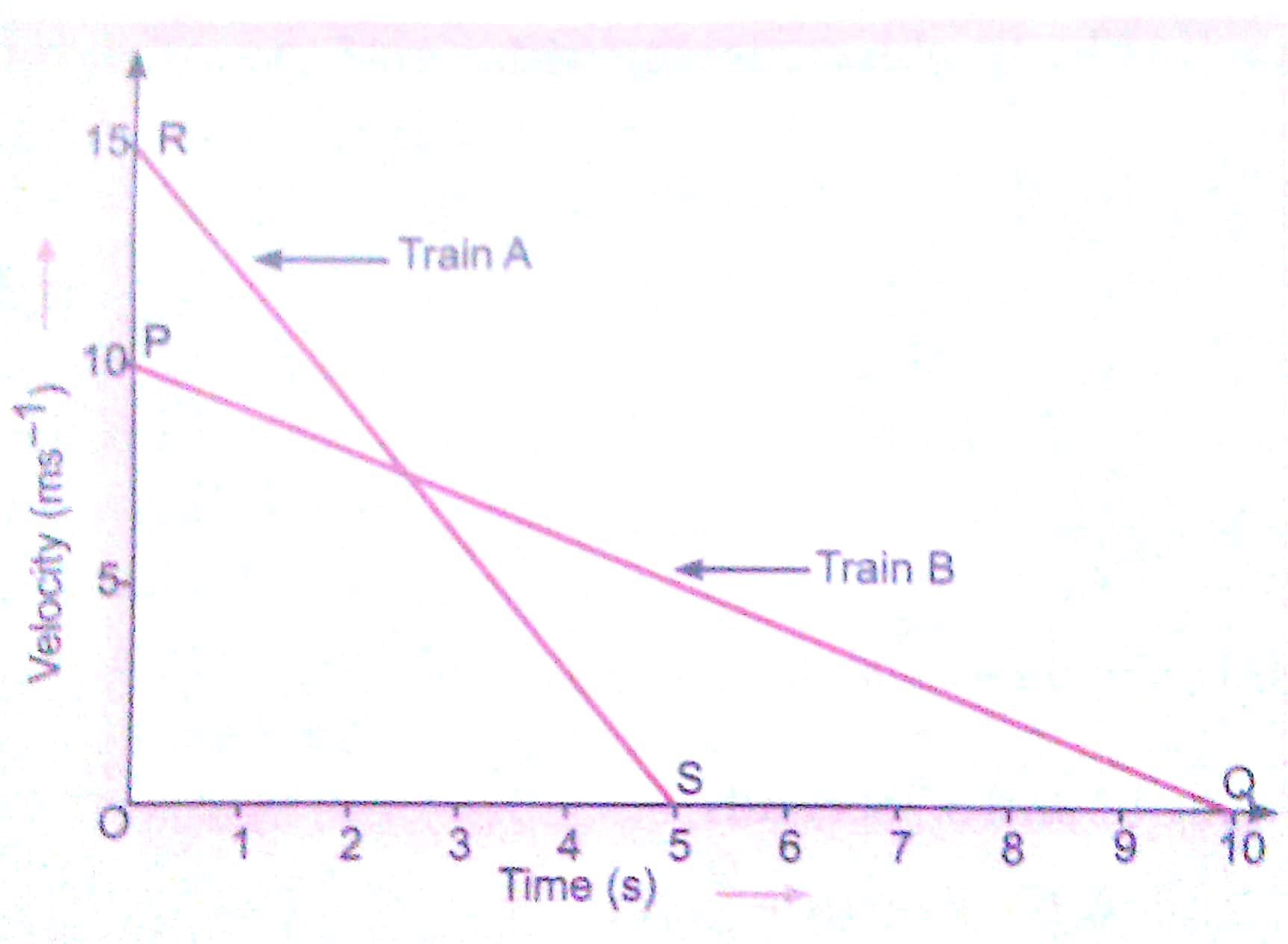
Distance travelled by train A
                       = Area under straight line graph RS
                     = Area of ΔORS

Distance travelled by train B = Area under PQ =  Area of ΔOPQ

Thus, train B travelled farther after the brakes were applied.